Wireless Communications
Radio broadcasting was perhaps the first successful wireless application. Other important examples of wireless applications have been, and still are, television broadcasting and satellite communication. However, the establishment of the first generation cellular phones back in the early 1980s has undoubtedly been the main initiator of the adrenaline boosting research race we are experiencing in wireless communications today.
The main question in wireless communication is how to design systems that allow communication with low error probability, high speed, and low cost. It has been shown that the quality of radio transmission over fading channels can be increased by introducing multiple antennas both at the transmitting end (e.g. a base station) and receiving end (e.g. a mobile phone).

Such wireless transmission can be put into action by using space-time block codes (STBC). A space-time code is a finite collection of complex matrices - usually of the same type, e.g. square 2x2 matrices as in the famous Golden code. The number of matrix rows equals the number of transmit antennas, and the number of columns is the transmission delay. The notion of a space-time code and the rank and determinant criteria for constructing such codes were set forth by Guey et al. and Tarokh et al. in 1996--1998. Soon after this began an enormous hunt for well-performing space-time codes resulting in further construction criteria, the most important of these being the diversity-multiplexing gain tradeoff (Tse et al.). In a similar fashion as the fundamental theorems in information theory by Claude Shannon, this tradeoff tells us that higher throughput can be achieved, but at the cost of an increased error probability and vice verse.
Interestingly, it has turned out that very sophisticated tools from algebraic number theory and further from class field theory are needed in order to satisfy the above criteria. Class field theory has enabled us to produce a general framework for the space-time code construction by providing us with powerful enough tools to measure the quality of the codes by means other than computer simulations. The concepts that are most commonly used involve cyclic division algebras, their maximal orders and discriminants.
Our research group has designed numerous world-record space-time codes (in terms of the block error rate) for different types of channels and different numbers of users, which should make the power of class field theory evident.
In the figure below is depicted the error performance of the Golden lattice space-time code (Oggier et al.) and the Golden+ code (the Turku team) in a Rayleigh fading channel with two transmit and two receive antennas. The lower the curve, the better the code.
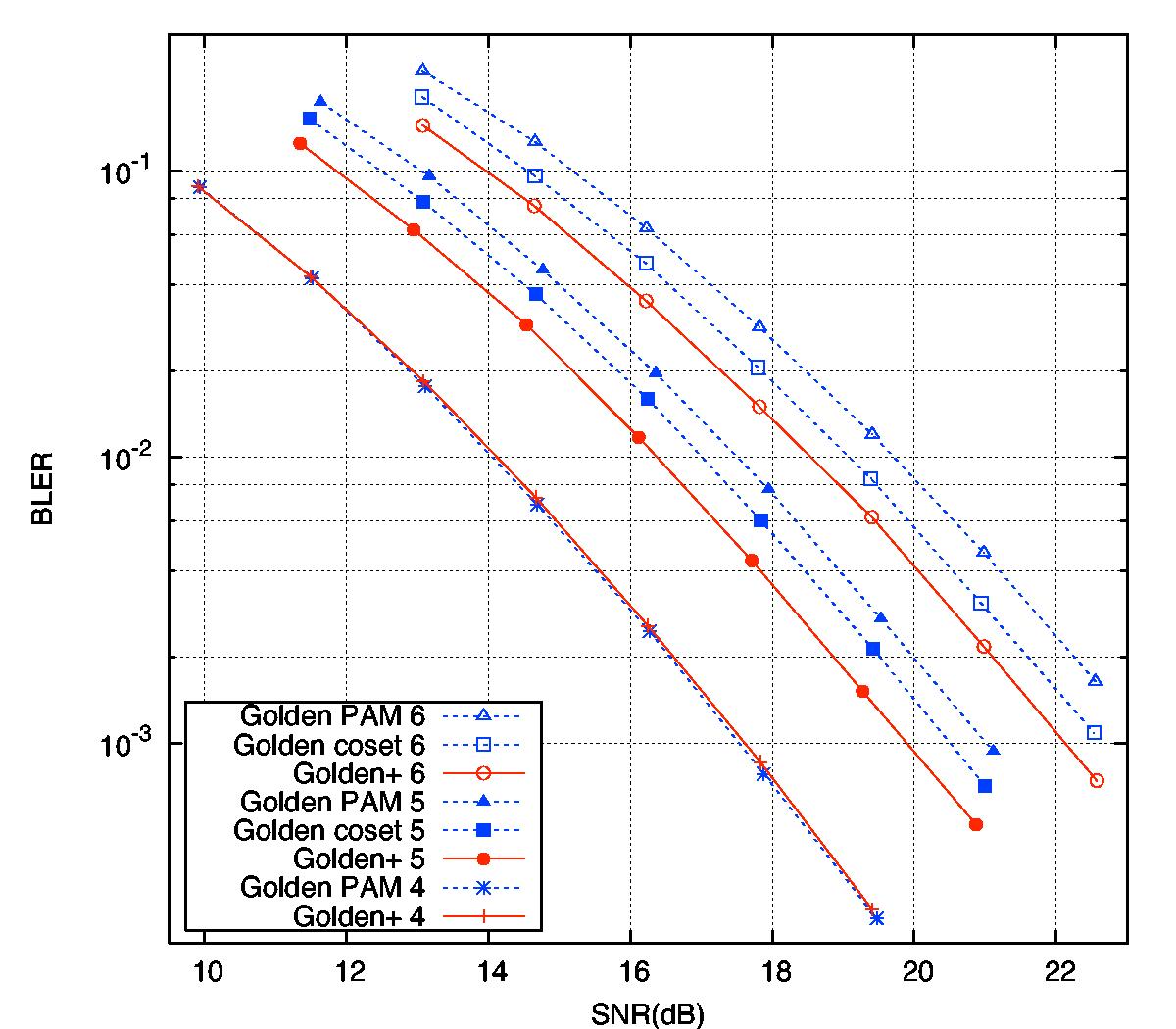
Block error rates of the Golden and Golden+ codes.