Coding Theory
– Identifying Codes
Let G = (V,E) be a connected undirected graph, finite or not. The distance between two vertices x and y is defined to be the length of any shortest path between x and y, and B(x) denotes the set of all vertices within distance 1 from x. We say that a subset C of the vertex set is an identifying code if the intersection of sets B(x) and C are nonempty and different for all vertices x.
This problem was introduced in 1998 by Karpovsky, Chakrabarty and Levitin [8], with the motivation of finding malfunctioning processors in multiprocessor architectures.
A closely related, earlier problem is that of studying locating-dominating sets introduced by Slater [10]: a subset C of the vertex set is called a locating-dominating set if the intersection of sets B(x) and C are nonempty and different for all x not in C.
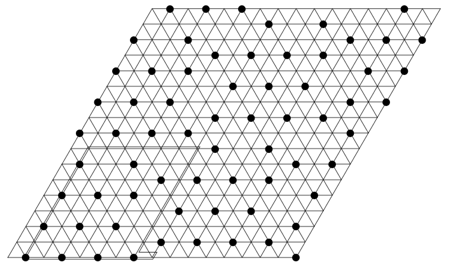
We have, for instance, proved that the smallest possible density of a locating-dominating set in the infinite triangular grid is 13/57; see [4]. An example of such a set is given in the figure. For many other results, see the papers listed below and in the list of journal papers of the group.
References:
- David Auger, Irène Charon, Iiro Honkala, Olivier Hudry and Antoine Lobstein, Edge number, minimum degree, minimum independent set, radius and diameter in twin-free graphs, Adv. Math. Commun. 3:97-114, 2009.
- Uri Blass, Iiro Honkala, Simon Litsyn, Bounds on identifying codes, Discrete Math. 241:119-128, 2001.
- Geoffrey Exoo, Ville Junnila, Tero Laihonen, Sanna Ranto, Upper bounds for binary identifying codes, Adv. in Appl. Math. 42:277-289, 2009.
- Iiro Honkala, An optimal locating-dominating set in the infinite triangular grid, Discrete Math. 306:2670-2681, 2006.
- Iiro Honkala, Mark G. Karpovsky and Lev B. Levitin, On robust and dynamic identifying codes, IEEE Trans. Inform. Theory, 52:599-612, 2006.
- Iiro Honkala, Tero Laihonen, On identifying codes that are robust against edge changes, Inform. and Comput. 205:1078-1095, 2007.
- Svante Janson, Tero Laihonen, On the size of identifying codes, J. Combin. Theory A 116:1087-1096, 2009.
- Mark G. Karpovsky, Krishnendu Chakrabarty and Lev B. Levitin, On a new class of codes for identifying vertices in graphs, IEEE Trans. Inform. Theory, 44:599-611, 1998.
- Tero Laihonen, Sequences of optimal identifying codes, IEEE Trans. Inform. Theory 48:774-776, 2002.
- Peter J. Slater, Dominating and reference sets in a graph, J. Math. Phys. Sci. 22:445-455, 1988.