Printable version (pdf)
Divisibility Problem for one relator
Monoids
S.I.Adian
Steklov Mathematical Institute
Gubkina str. 8, 117966 Moscow, RUSSIA
e-mail: si@adian.mian.su
We consider monoids presented
by one defining relation in 2 generators:
M = < a, b; aU = bV>.
(1)
Denote A1 = aU
and A2 = bV.
We say that the word X is
left
side divisible by Y in M if there exists a word
Z
such that X = YZ in M. The left side divisibility problem
for M is the requirement to find an algorithm to recognize for any
two words X and Y, whether or not X is left side divisible
by Y in M?
The following theorem was proved
in [1,2,3].
Theorem 1 The word
problem for any 1-relator monoids can be reduced to the left side divisibility
problem for monoids M presented in 2 generators by 1 defining relation
of the form aU = bV. For the solution of this problem it sufficies to find
an algorithm to recognize for any word aW (or for any word bW) whether
or not it is left side divisible in M by the letter b (accordingly by the
letter a).
Algorithm 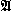
The algorithm  was introduced in [2] for a more general case of monoids presented by any
cyclefree system of relations. Here we shall apply this algorithm to the
case of the monoid
M.
was introduced in [2] for a more general case of monoids presented by any
cyclefree system of relations. Here we shall apply this algorithm to the
case of the monoid
M.
The algorithm  was used in several papers for a solution of the left side divisibility
problem for monoids M under some additional conditions.
was used in several papers for a solution of the left side divisibility
problem for monoids M under some additional conditions.
To apply this algorithm one should
find another algorithm  that
decides for any word aW, whether or not the algorithm
that
decides for any word aW, whether or not the algorithm  terminates when applied to aW.
terminates when applied to aW.
For the given word aW the
algorithm  finds the uniquely
defined prefix decomposition which is either of the form
finds the uniquely
defined prefix decomposition which is either of the form
aW = P1P2
... PkPk+1,
(2)
where each Pi is
the maximal nonempty proper common prefix of the word PiPi+1
... Pk+1 and the appropriate relator aU or bV,
or of the form
aW = P1P2
... PkAjkWk+1,
(3)
where the prefixes Pi
are defined in a similar way, but the segment Ajk
is one of the relators of the monoid M. We call the segment Ajk the
head of the decomposition (3).
Let us describe in details how our
algorithm  works.
works.
Suppose we have an initial word aW.
Consider the Maximal Common Prefix of two words aW and A1
and denote it by
P1 = MCP(aW,
A1).
(4)
We have aW = P1W1
and aU = P1U1 for some W1
and U1.
Clearly P1 is not
empty. We consider the following 2 cases.
Case 1. If U1 is
empty, then aW = aUW1. So we have a prefix decomposition
of the form (3) for k=0.
In this case the algorithm  replaces in aW the segment aU by bV. So we obtain
aW
= bVW1 in M. Hence aW is left side divisible
by b in M.
replaces in aW the segment aU by bV. So we obtain
aW
= bVW1 in M. Hence aW is left side divisible
by b in M.
Case 2. Let U1
be not empty. Then P1 is a proper prefix of aU.
If W1 is empty
then aW is a proper segment of the relator aU. It is easy
to prove that the proper segment P1 of aU is not
divisible by b in M.
Hence we can assume that U1
and W1 both are nonempty. It follows from (4) that in
this case they have different initial letters a and b.
In this case to prolong the prefix
P1
of aU in P1W1 to the right side we
should divide W1 by b if it starts by a
or divide W1 by a if it starts by b. So
the situation is similar to the initial one.
Now in a similar way we consider
the nonempty word P2 = MCP(W1 , Aj),
where Aj1
is the relator of M which has a common initial letter with W1.
Suppose W1 = P2W2
and Aj = P2U2. Then again we consider
2 cases.
Case 2.1. If U2
is empty, then W1 = AjW1.
In this case we have the following
prefix decomposition of the word aW:
aW = P1Aj1W2,
where Aj1
is called the head.
Case 2.2. Let U2
be nonempty.
In this case if W2
is empty then aW = P1P2 where P2
is a proper segment of of the relator Aj1
.
Hence we obtained for aW a prefix decomposition of the form (2).
It is easy to prove that the word P1P2 is
not divisible by b in M.
Hence we can assume that U2
and W2 both are nonempty. It follows from (4) that in
this case they have different initial letters a and b.
In this case to prolong the prefix
P2
of Aj1 in
P1P2W2
we should divide W2 by b if it starts by a,
or divide
W2 by
a if it starts by b. So
the situation again is similar to the initial one.
Hence we can consider the nonempty
word P3 = MCP(W2 , Aj2
),
where Aj2 is
one of the relators of M which has the common initial letter with
the word W2. And so on. The length of the word Wi
is decreasing. So after a finite number of steps either we shall find some
prefix decomposition of the form (3) with the head Ajk
or we shall stop on some decomposition of the form (2).
It is easy to prove that if the decomposition
of aW is of the form (2), then the word aW in M is
not left side divisible by b.
If the decomposition is of the form
(3), then the algorithm  replaces
the head Ai in aW by the another relator in (1):
aU
should be replaced by bV or bV by aU. Hence we get
one of the following elementary transformations in the monoid
M:
replaces
the head Ai in aW by the another relator in (1):
aU
should be replaced by bV or bV by aU. Hence we get
one of the following elementary transformations in the monoid
M:
aW = P1P2
...PkaUWk+1®
P1P2 ...PkbV Wk+1 = W'
or
aW = P1P2
...PkbVWk+1®
P1P2 ...PkaUWk+1 = W'.
Clearly the result W' of this
transformation is equal to aW in M. If the resulting word
W'
starts by the letter b (this happens only if k=0!), then
the algorithm  terminates by
the positive answer. Otherwise the algorithm
terminates by
the positive answer. Otherwise the algorithm  repeats the same procedure with the word W'.
repeats the same procedure with the word W'.
Theorem 2 (see [2])
If the word aW is left side divisible by b in M then the algorithm  (aW)
terminates with the positive result, and in this case we obtain the shortest
proof of the left side divisibility of the word aW by b in M.
(aW)
terminates with the positive result, and in this case we obtain the shortest
proof of the left side divisibility of the word aW by b in M.
Conjecture 1 There
exists an algorithm  that decides
for any word aW whether or not the algorithm
that decides
for any word aW whether or not the algorithm  (aW)
terminates.
(aW)
terminates.
Problem 1 Check if
the conjecture 1 is true.
REFERENCES
1 Adian S.I.
(1966). Defining relations and algorithmic problems for groups and semigroups.
Proc. Steklov Inst. Math. 85. (English version published by the
American Mathematical Society, 1967).
2. Adian S.I. (1976).
Word transformations in a semigroup that is given by a system of defining
relations. Algebra i Logika
15, 611-621; English transl. in
Algebra and Logic 15 (1976).
3. Adian S.I. and
Oganesian G.U. (1987). On the word and divisibility problems in semigroups
with one defining relation. Mat. Zametki 41, 412-421; English transl.
in Math. Notes 41 (1987).
4. Adian S.I. and
V.G.Durnev. Decision problems for groups and semigroups. In "Russian Math.
Surveys" (Uspechi Mat. Nauk, 2000), vol. 55, No. 2, pp. 207-296.



