 |
Miksi netti tökkii?
Kaaret solmussa
|
Kerhoillan tarkoituksena on perehtyä konkreettisten esimerkkien avulla verkkoteorian peruskäsitteisiin. Toiminta tapahtuu sekä ryhmissä, että yksintyöskentelynä. Lisää motivaatiota haetaan kilpailun avulla. Aluksi voidaan käydä verkkojen perustermejä läpi kuvien avulla ja lopuksi (suurimman osan kerhoillasta) pelataan pelejä, joissa sovelletaan verkkoteoriaa.
Mikä on verkko? (Kaikkia termejä ei tarvitse/kannata opettaa, mielenkiinnon ja oppilaiden tason mukaan)
- Verkko on joukko pisteitä, joita yhdistävät viivat.
- Pisteitä kutsutaan solmuiksi ja viivoja kaariksi.
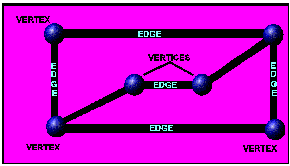
- Kaaria voi olla mielivaltainen määrä (myös nolla) ja ne voivat kulkea mistä solmusta mihin solmuun tahansa, myös takaisin itseensä.
- Kaaret voivat olla suunnattuja, jolloin niitä pitkin päästään vain toiseen suuntaan. Tällöin puhutaan suunnatusta verkosta.
- Jokapäiväinen esimerkki verkosta on esim. kartta: tiet ovat kaaria ja solmut teiden risteyksiä (yksisuuntaiset kadut ovat suunnattuja kaaria).
- Solmun aste on siitä lähtevien kaarien lukumäärä.
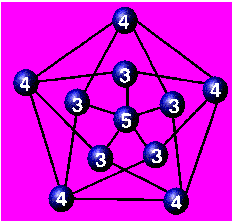
- Verkon koko on sen solmujen lukumäärä.
- Verkko on säännöllinen, jos jokaisen solmun aste on sama.
- Polku on reitti, jota pitkin päästään jostakin solmusta johonkin toiseen solmuun kaaria pitkin kulkien.
- Sykli on polku, joka loppuu samaan solmuun kuin mistä se alkoi.
- Polun pituus on kaarien lukumäärä polulla (onko se sama kuin solmujen lukumäärä polulla?).
- Hamiltonin polku on polku, joka kulkee verkon jokaisen solmun läpi täsmälleen kerran. Kaikkia kaaria ei välttämättä kuljeta. Jos polulla on sama alku- ja loppusolmu sanotaan polkua Hamiltonin sykliksi. Tunnetussa kauppamatkustajan ongelmassa etsitään (lyhintä) Hamiltonin sykliä annetussa verkossa.
- Eulerin polku puolestaan kulkee jokaisen kaaren yli täsmälleen kerran. Polku voi mennä saman solmun kautta useammankin kerran. Jos polulla on sama alku- ja loppusolmu sanotaan polkua Eulerin sykliksi. Sovelluksena voisi mainita tilanteen, jossa kaupungin katujen keskiviivat pitää maalata kerralla uusiksi.
- Etäisyys kahden solmun välillä on kaarien lukumäärä niitä yhdistävällä (lyhimmällä) polulla.
- Täydellisessä verkossa kaikkien solmujen välillä on kaari. Tällaisella verkolla voidaan esim. laskea, montako kättelyä suoritetaan tilaisuudessa, jossa kaikki kättelevät keskenään tai montako peliä pelataan sählyturnauksessa, jossa kaikki pelaavat kaikkia vastaan kerran: jokaista joukkuetta vastaa solmu ja pelattua peliä kaari (kukin kaari lasketaan vain kerran).
- Solmun naapureita ovat kaikki ne solmut, jotka on yhdistetty kaarella ko. solmuun (kahden naapurisolmun etäisyys on siis aina 1 ja täydellisessä verkossa kaikki solmut ovat naapureita keskenään).
Termit selityksineen ja lisäkuvia:
http://www.c3.lanl.gov/mega-math/workbk/graph/grvocab.html
Tehtävä 1: Nettipeli
Toimintamuoto: Toimitaan ryhmänä
Toiminnan kuvaus: Peli havainnollistaa tietoverkon reititysongelmia ja lukkiutumista. Kukin oppilas esittää viestiä, jolla on määränpää. Päästäkseen määränpäähänsä viesti voi liikkua reittiä pitkin vain kun se on vapaa. Koska kaikki yrittävät päästä määränpäähänsä, tarvitaan yhteistyötä tehtävän onnistumiseksi.
Tarvittavat välineet:
- Narua
- Maalarinteippiä
- Pallo
- Paperikiekot solmuiksi
- Määränpäälaput
Mitä ohjaajan tulee tietää?
Pelaajien lukumäärästä
- Peli on haastavin, kun pelaajia on yksi vähemmän kuin verkossa on solmuja. Pelaajien vähentäminen tai pallojen lisääminen helpottaa peliä (miksi? Koska se lisää liikkumisvaihtoehtoja).
Alkuasetelma
- Valmistetaan kortteja, jotka täsmäävät solmujen nimien kanssa. Kortit voidaan esim. kiinnittää vaatteisiin tai ripustaa kaulaan.
- Solmut nimetään yksilöllisesti, kirjaimella, numerolla, paikannimellä tai vastaavasti.
- Pelaajat seisovat solmuissa ja heittävät ja ottavat kiinni palloa. Verkon on oltava tarpeeksi pieni, jotta pallon heittäminen verkon yli onnistuu.
Miten pelataan:
- Pelaajat asettuvat verkon solmuihin. Ainakin yksi solmu jätetään tyhjäksi.
- Kortit jaetaan pelaajille satunnaisesti.
- Pallo annetaan yhdelle pelaajista.
- Pelin tarkoitus on, että kukin pelaaja pääsee siihen solmuun, joka kortissa on nimetty.
- Pelaaja voi liikkua kaaria pitkin solmusta toiseen vain, jos:
- Hänellä on pallo.
- Solmu, johon hän on siirtymässä, on tyhjä.
- Pelaaja, jolla on pallo, voi heittää pallon kenelle tahtoo.
- Se joukkue, joka on "oikeassa järjestyksessä" (eli jokainen pelaaja kohdesolmussaan) nopeimmin (tai vähimmillä siirtymisillä), voittaa.
Huom: tarkoituksena pelata peli useammin (pari kertaa). Ensin demonstroiden laajakaistaa (useampia tyhjiä solmuja) ja sitten modeemiyhteyttä (vähemmän tyhjiä solmuja).
Tehtävä 2: Turistikaupunki
Toimintamuoto: Toimitaan ryhmänä.
Tehtävän kuvaus: Verkko saadaan aikaiseksi liikuntasalin lattialle käyttämällä esim. maalarinteippiä ja narua. Solmut merkitään aluksi pahvilapuilla. Verkko kuvaa tässä tehtävässä kaupunkia, jossa jokainen solmu on talo ja jokainen polku on katu. Kaupunkiin tulee turisti, joka haluaa käydä kaikissa taloissa. Jotta hän ei tuhlaisi turhaa aikaa, kaupunki on päättänyt maalata talot niin, ettei yksikään vierekkäinen talo (eli solmu) ole samanvärinen kuin mikään sen naapuri. Näin turisti tietää, missä taloissa hän on käynyt. Kaupungilla on pieniä taloudellisia ongelmia ja kaikessa pitää säästää, eli mikä on pienin maalivärien lukumäärä (ts. montako eri väriä tarvitaan) joilla koko kaupunki saadaan maalattua edellä kuvatulla tavalla?
Mitä ohjaajan tulee tietää?
- Eriväriset pahvikiekot kuvaavat maalattuja taloja. Oppilaiden tehtävänä on sijoittaa maalatut talot verkkoon. Kannattaa kiinnittää huomiota verkon kokoon.
Tarvittavat välineet
- Maalarinteippiä
- Narua
- Pahvikiekkoja
Tehtävä 3: Jäätelökioskiongelma
Toimintatapa: Yksintyöskentely
Tehtävänkuvaus: Tässä tehtävässä verkkoa käytetään esittämään kaupungin karttaa. Ongelma, joka tarinassa selitetään, on helppo ymmärtää, mutta yksinkertaista, suoraviivaista ratkaisua ongelmaan ei ole olemassa. Oppilaat löytävät kokeilemalla erilaisia lähestymistapoja ongelmaan.
Tarvittava materiaali:
- Kopio kaupungin kartasta jokaiselle oppilaalle (muutama eri tasoinen tehtävä; mitä enemmän solmuja (taloja), sitä vaikeampi tehtävä).
- Kalvo kaupungin kartasta ja ratkaisusta, jotka voidaan näyttää piirtoheittimellä
lopuksi.
Ohjeet:
- Oppilaille jaetaan kartat ja kerrotaan seuraava tarina (suomenna itse oman maun mukaan):
What you have in your hands is a map of the town of Iceberg. It's a somewhat unusual way to draw a map. The lines on this map represent streets and the dots are street corners. The map doesn't have any houses on it, but we do know that there is at least one house at each corner.
Iceberg would be a nice place to live, except for one problem: you can't get ice cream anywhere in town. So Ivan and Ivana Icicle have founded the The Icicle & Iceberg Ice Cream Company in order to do something about that. Ivan and Ivana want to do something good for their town, so they are going to build ice cream stands all over town where people can go to buy ice cream. They want it to be easy for the people to get ice cream. They also want to make money.
At first, Ivan and Ivana had hoped to put an ice cream stand on every corner, knowing how, in the summertime, they would just rake in the money. But ice cream stands are expensive to build: you have to buy all that lumber, and nails, and windows, etc. Then you have to put big freezers inside them, and pay people to work in them all day, and so forth. It didn't seem possible to sell enough ice cream to pay for ice cream stands on every corner.
They figured, however, that people would still eat lots of ice cream if they only had to walk down the street to get it. Their second plan was to build the ice cream stands so that people could get ice cream either right there on the corner where they live, or at the very most, have to walk down only one street to find a corner where there was an ice cream stand.
- Oppilaiden pitää siis sijoittaa jäätelökioskit kartalle.
- Miten ne pitäisi asettaa?
- Paljonko kioskeja tarvitaan?
- Oppilaille näytetään tarvittavat merkinnät: kioskit merkitään esim. neliöillä ja kaikki ne kadunkulmat, jotka ovat yhden kadunvälin päässä kioskista esim. kolmioilla.
- Kannattaa käyttää lyijykynää, jotta tehtävää voi yrittää useamman kerran samaan karttaan.
- Oppilaille muistutetaan, että kioskit ovat kalliita, joten niiden määrä pitäisi minimoida.
- Voidaan kertoa, että 6 kioskia riittää.
- Kun kaikki ovat ratkaisseet ongelman tavallaan, heille näytetään ratkaisu.
Ohjaajalle tiedoksi: Kyseinen ongelma on esimerkki tapauksesta, jossa etsitään verkon hallitsevaa joukkoa (dominating set): verkon hallitseva joukko muodostuu niiden solmujen minimaalisesta joukosta, jotka naapureineen kattavat kaikki verkon solmut. Ao. Kuva selventää käsitettä:
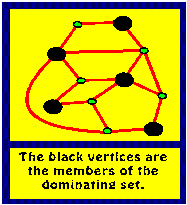
Lisätietoja:
http://www.c3.lanl.gov/mega-math/workbk/graph/grother.html (tehtävät 1 ja 2)
http://www.c3.lanl.gov/mega-math/workbk/dom/doice.html (tehtävä 3)




